ToTo Man
the band not the dog
I'm never quite sure what window and FFT I should be using when examining the frequency spectra of audio samples in Audacity. I realise it's a technically complex topic of which I have very limited understanding of, so detailed explanations are likely to be lost on me. All I really need to know is what Window and FFT I should use in the following scenarios:
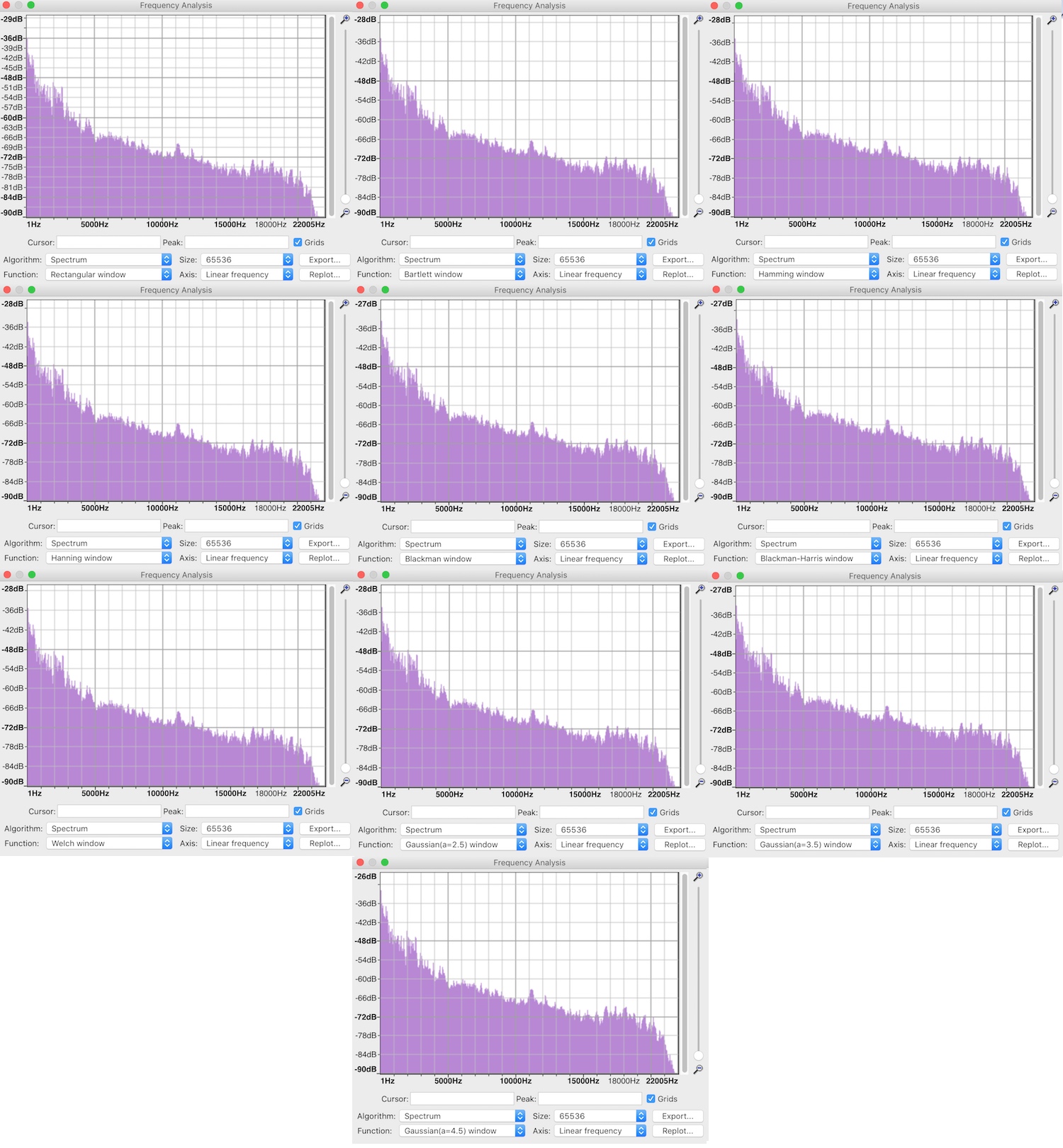
1) White Periodic Noise:
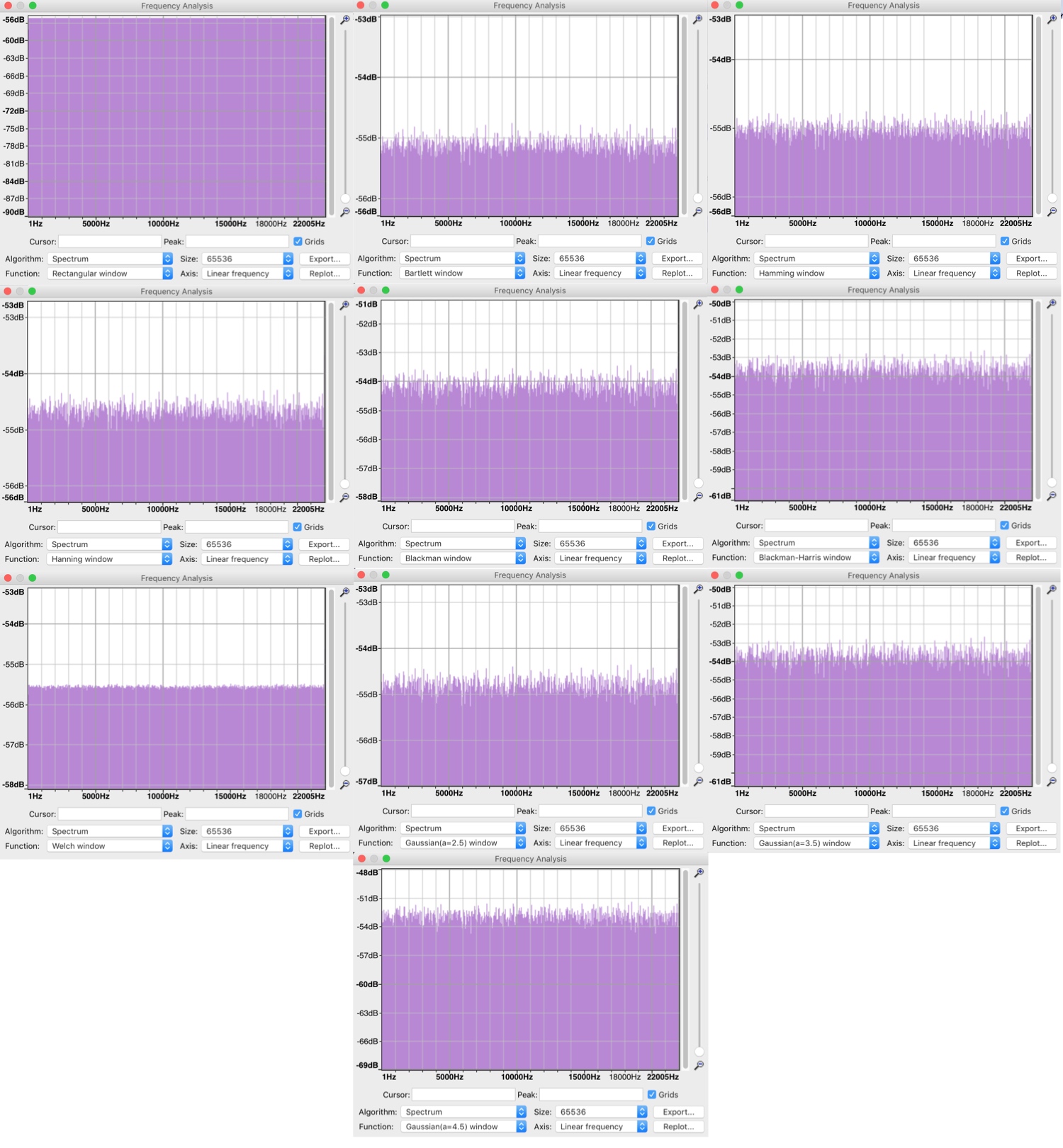
If I export a sample of White Periodic Noise with FFT of 65536 from REW, it looks smoothest when viewed with a Rectangular window and FFT of 65536, with these settings it displays as a perfectly flat line with zero scribbling.
(When I output this signal to my DAC route it back into my Focusrite 4i4, the line becomes slightly scribbled and is no longer perfectly flat. The Welch window displays a slightly flatter line than the Rectangular, but I assume I should still use the Rectangular window?)
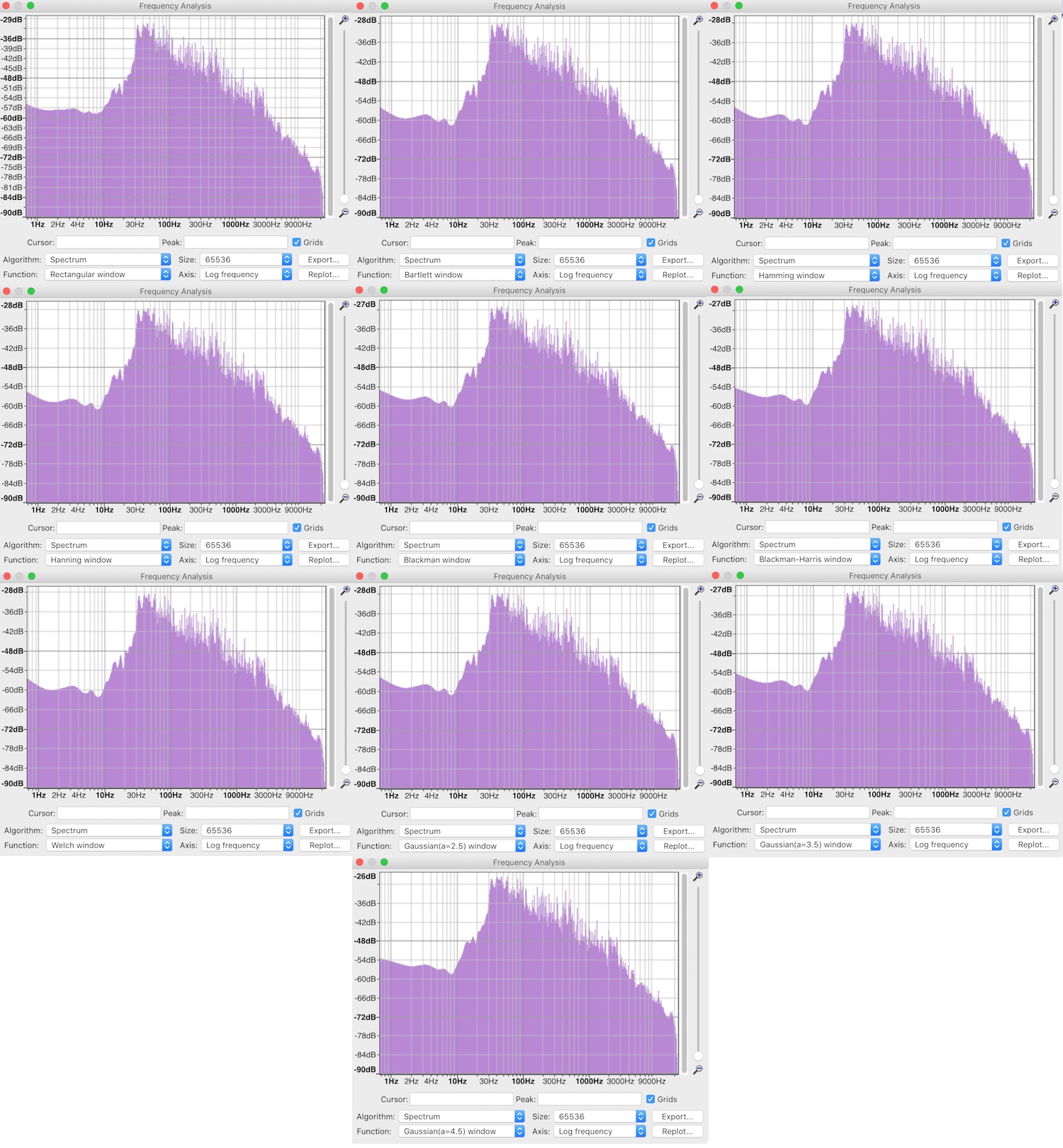
2) Pink Periodic Noise:
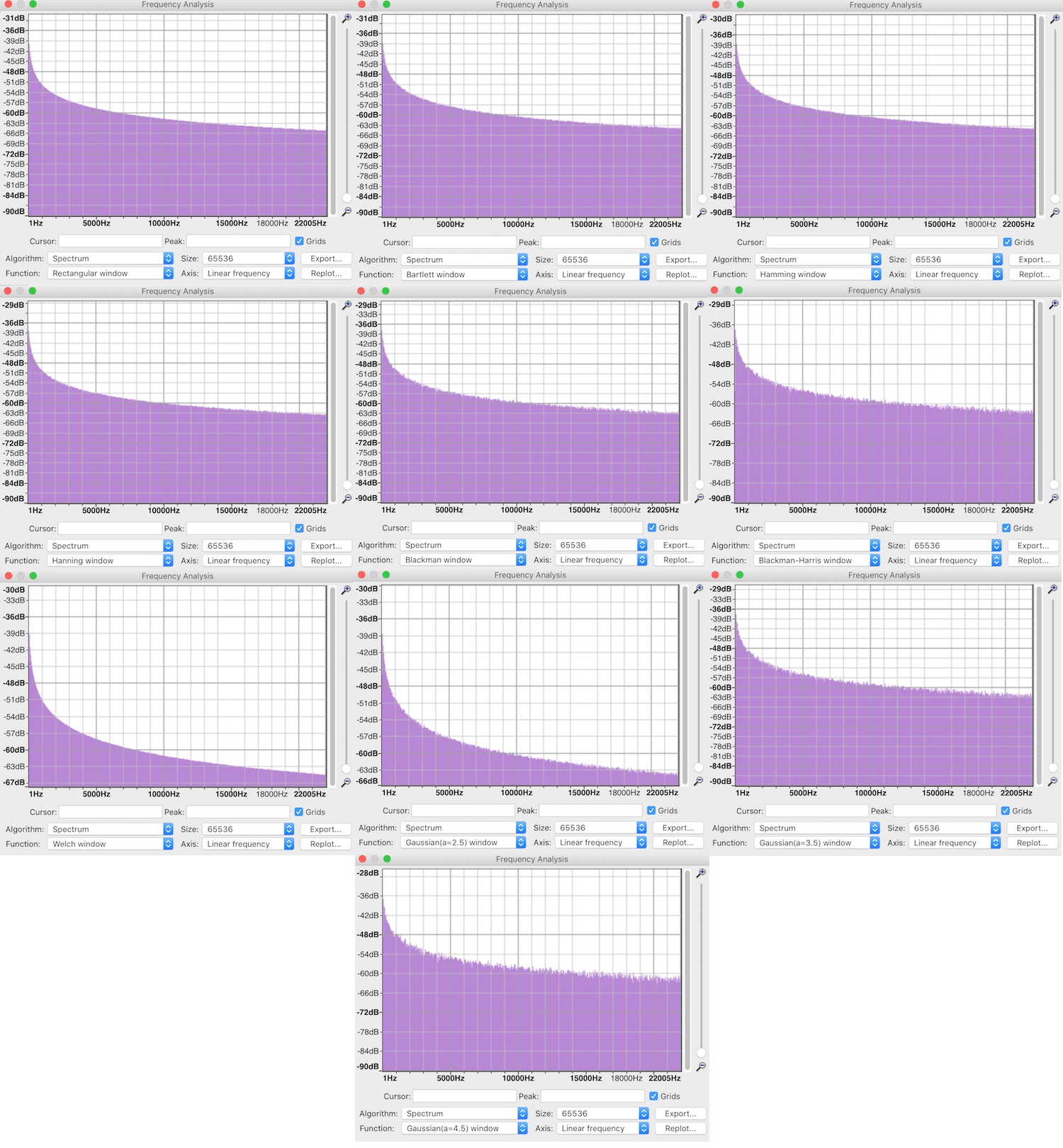
If I generate a sample of Pink Periodic Noise with FFT of 65536 in REW then analyse it in Audacity, it looks equally smooth when viewed with Rectangular or Welch windows with FFT of 65536. The other Window functions introduce scribbling.
3) Log and linear sine wave sweeps:
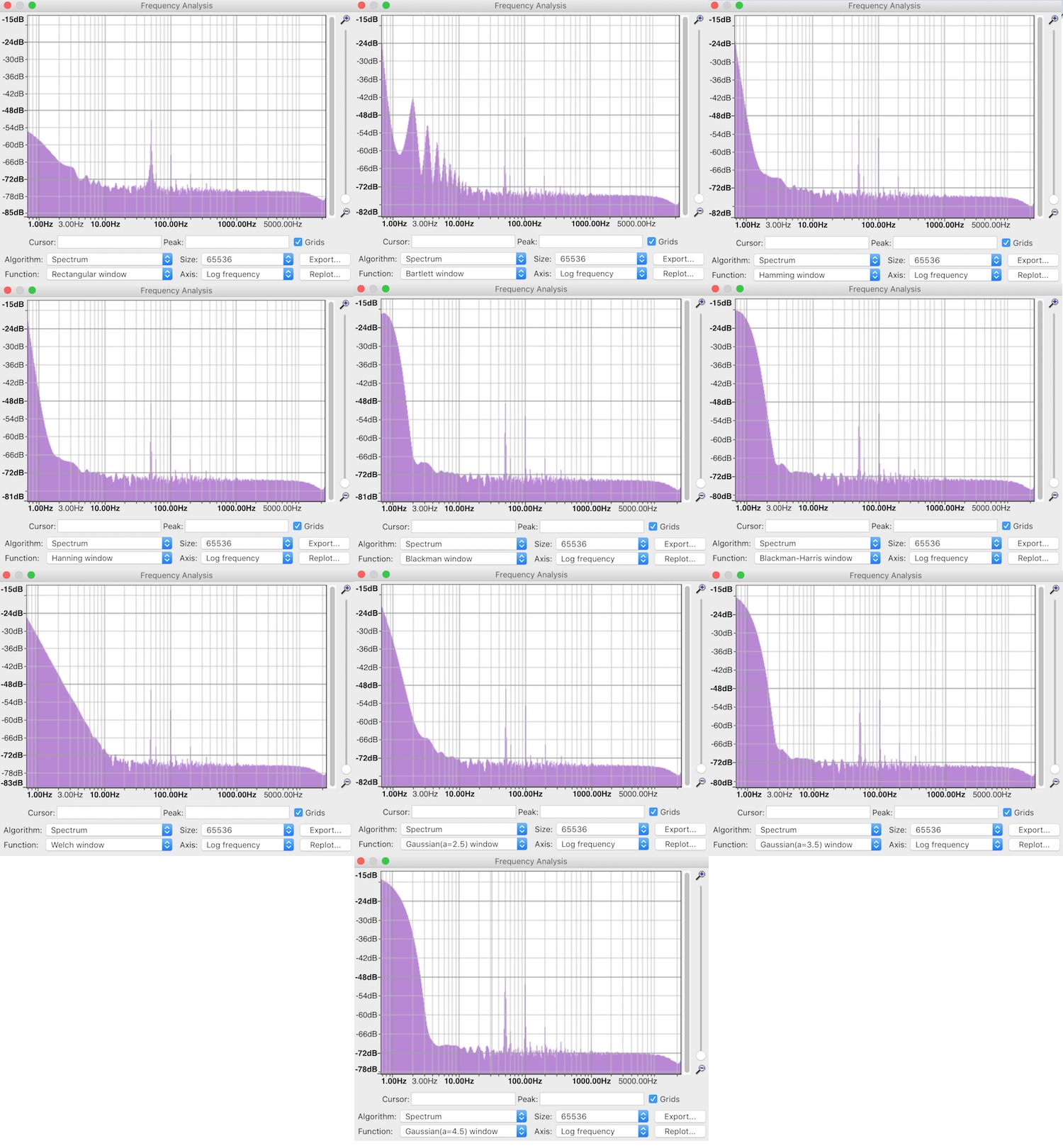
If I export a linear or log sine wave sweep from REW, no combination of Window and FFT in Audacity displays as a smooth or flat lines throughout the entire frequency range, some are 'sawtooth' in appearance and others have square 'steps'.
4) If I want to analyse the noise floor of an analogue input, what Window and FFT is most appropriate?
5) If I want to analyse the frequency content of music, what Window and FFT provides the most accurate representation?
1) White Periodic Noise:
If I export a sample of White Periodic Noise with FFT of 65536 from REW, it looks smoothest when viewed with a Rectangular window and FFT of 65536, with these settings it displays as a perfectly flat line with zero scribbling.
(When I output this signal to my DAC route it back into my Focusrite 4i4, the line becomes slightly scribbled and is no longer perfectly flat. The Welch window displays a slightly flatter line than the Rectangular, but I assume I should still use the Rectangular window?)
2) Pink Periodic Noise:
If I generate a sample of Pink Periodic Noise with FFT of 65536 in REW then analyse it in Audacity, it looks equally smooth when viewed with Rectangular or Welch windows with FFT of 65536. The other Window functions introduce scribbling.
3) Log and linear sine wave sweeps:
If I export a linear or log sine wave sweep from REW, no combination of Window and FFT in Audacity displays as a smooth or flat lines throughout the entire frequency range, some are 'sawtooth' in appearance and others have square 'steps'.
4) If I want to analyse the noise floor of an analogue input, what Window and FFT is most appropriate?
5) If I want to analyse the frequency content of music, what Window and FFT provides the most accurate representation?
Last edited: